Let's reveal the true shapes that a generative model make!
We introduce a dual contouring method that provides state-of-the-art performance for occupancy functions while achieving computation times of a few seconds. Our method is learning-free and carefully designed to maximize the use of GPU parallelization.
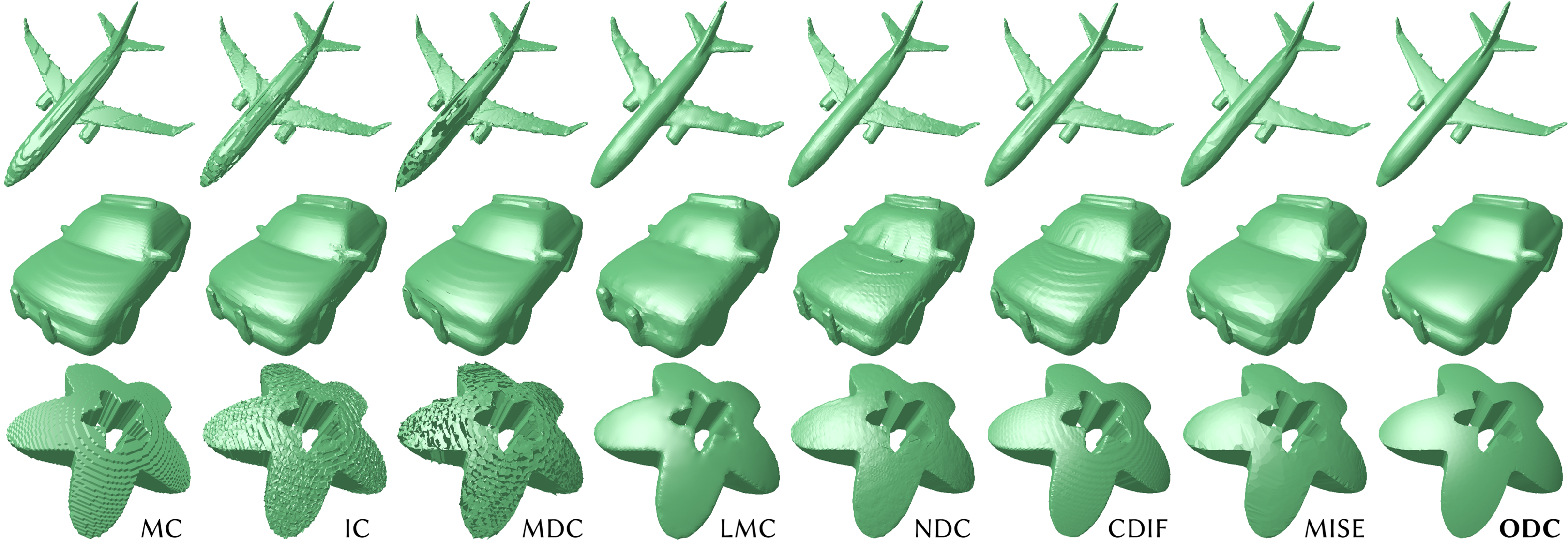
The recent surge of implicit neural representations has led to significant attention to occupancy fields, resulting in a wide range of 3D reconstruction and generation methods based on them. However, the outputs of such methods have been underestimated due to the bottleneck in converting the resulting occupancy function to a mesh. Marching Cubes tends to produce staircase-like artifacts, and most subsequent works focusing on exploiting signed distance functions as input also yield suboptimal results for occupancy functions.
Based on Manifold Dual Contouring (MDC), we propose Occupancy-based Dual Contouring(ODC), which mainly modifies the computation of grid edge points (1D points) and grid cell points (3D points) to not use any distance information. We introduce auxiliary 2D points that are used to compute local surface normals along with the 1D points, helping identify 3D points via the quadric error function. To search the 1D, 2D, and 3D points, we develop fast algorithms that are parallelizable across all grid edges, faces, and cells. Our experiments with several 3D neural generative models and a 3D mesh dataset demonstrate that our method achieves the best fidelity compared to prior works.
ODC maximally leverages continuous implicit functions to extract highly accurate surfaces, fully parallelizable on GPUs.
The method consists of five steps: Grid Sampling, 1D point search, 2D point search, 3D point identification, and polygonization.

1D point search identifies surface intersections along grid edges using binary search.
Then, sharp features (2D points) are detected on grid-aligned planes as accurately as possible using our 2D point search.
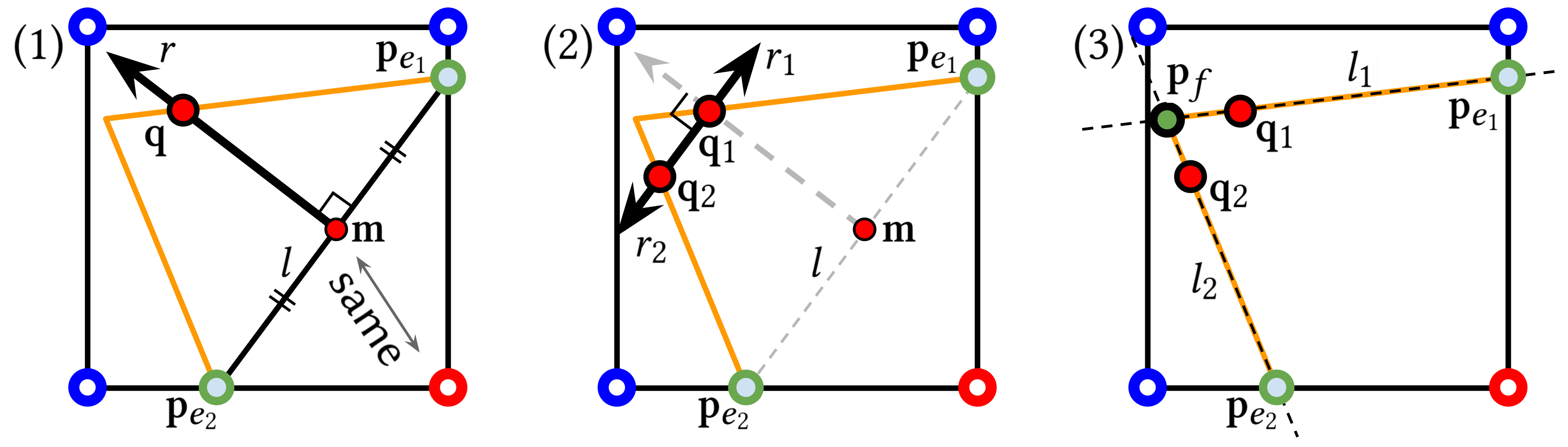
2D point search correctly detects the sharp feature \(p_f\) by doing three line-binary searches, as shown in the figure above.
For further details, please refer to our paper.
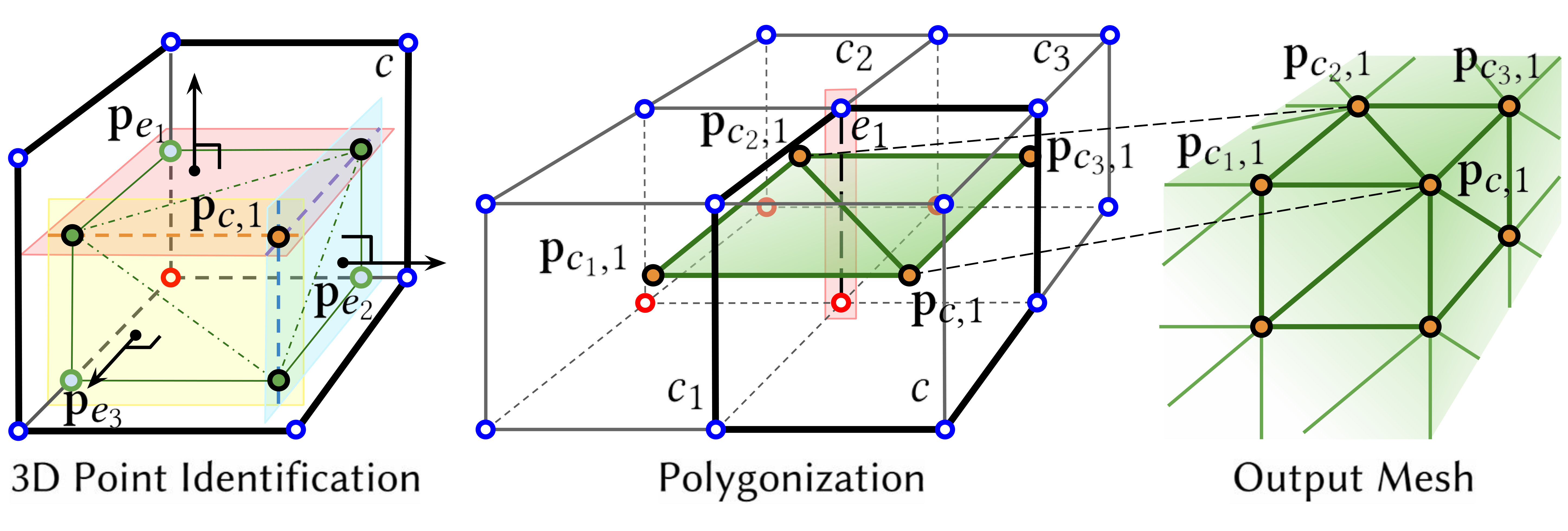
Unlike traditional methods like Manifold Dual Contouring,
Our method DO NOT require gradient information from the input implicit function.
We solve the Quadric Error Function (QEF) using only 1D and 2D points obtained in the previous steps,
and then perform polygonization following the Manifold Dual Contouring approach.
| Marching Cubes | Inters.-free Contouring | Manif. Dual Contouring | Lempitsky's method | Neural Dual Contouring | Contouring DIF | MISE | PoNQ | ODC (Ours) |
|---|



@inproceedings{hwang2024odc,
title = {Occupancy-Based Dual Contouring},
author = {Hwang, Jisung and Sung, Minhyuk},
booktitle = {SIGGRAPH Asia 2024 Conference Papers},
year = {2024}
}